Introduction and Overview

Given some information about the commands provided to the actuators of a robot and a dynamic model of the robot we, in theory, have enough information to make basic predictions about the motion of the robot. Can this information be useful for state estimation?

This paper claims to be able to incorporate control inputs to a drone in order to:

• Improve the accuracy of state estimation

• Estimate external forces (lots of potential applications if this is possible)

While the method should be robot agnostic, the paper is focused on MAVs. The control input we have access to is commanded rotor speed. We use a simple dynamic model which converts the rotor speed into a commanded thrust vector.

Background and Related Work

Deterministic Approaches

Assume that the measured acceleration from the IMU is composed of a commanded thrust and additive external force. Naively estimate external force as:

• Does not account for estimated IMU bias

• Can't account for noise on thrust estimation or IMU measurements

Probabilistic Approaches

• Uses filtering based technique (like a UKF) to estimate external forces

• State estimation is loosely coupled with external force compensation

Sliding Window Smoothing

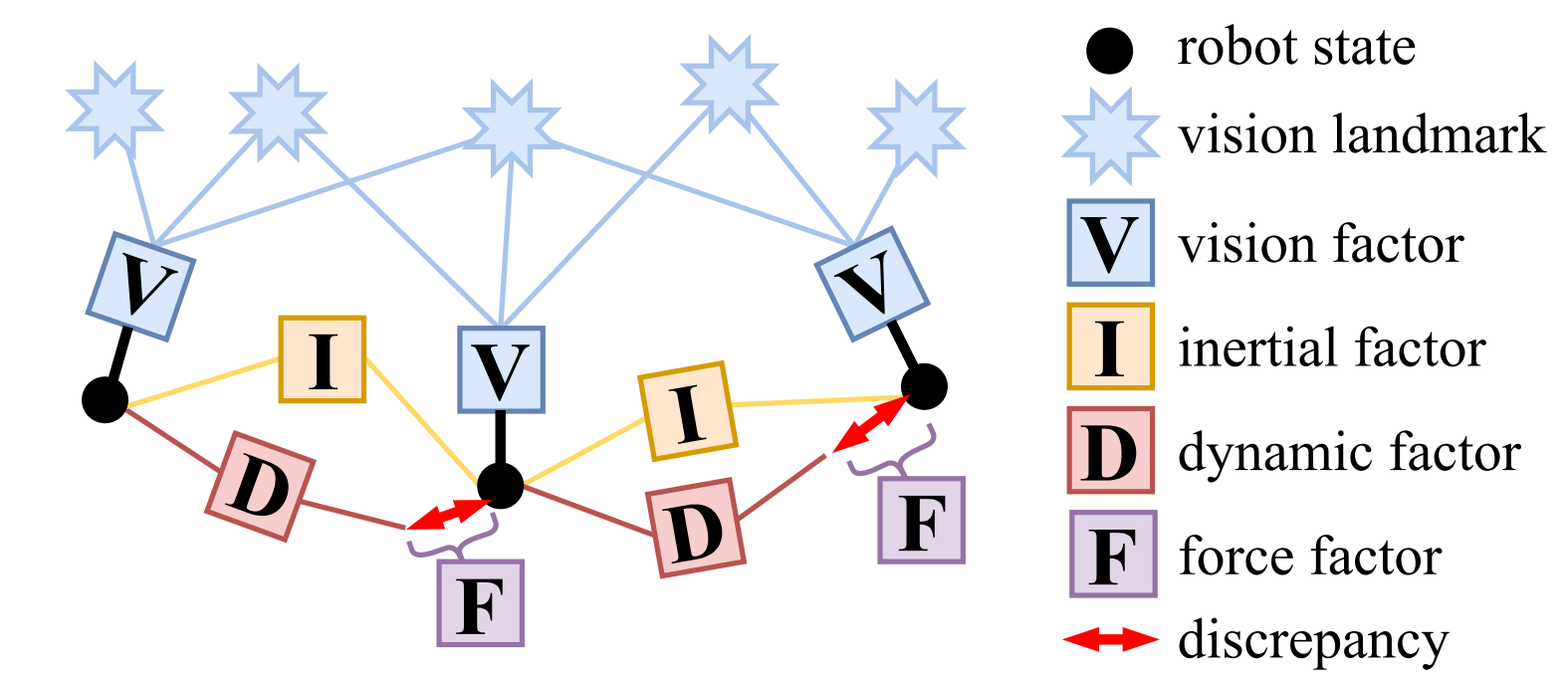
• Typical fixed-lag smoothing VIO with IMU pre-integration factors, landmark projection factors, and preintegrated dynamics factors

• In the presence of external forces, IMU biases and be incorrectly adjusted to account for the discrepancy between predicted motion from dynamic model and observed motion

Factor Graph Structure

Factor graph from paper:

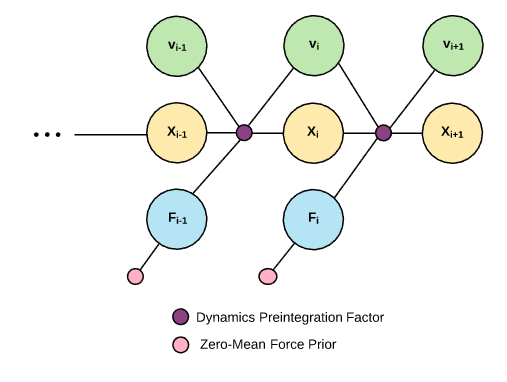
My best guess at factor graph structure of dynamics factor:

VIO factor graph is a modification of the VINS-Mono factor graph.

Pre-integrated Dynamics Factor

Like IMU preintegration, the goal of the preintegrated dynamics factor is to create a residual which can be evaluates without re-integration of control inputs when the linearization point changes.

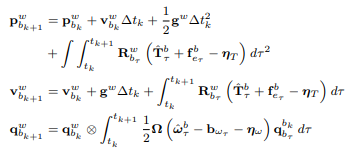
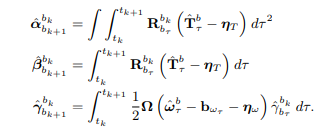
Residual

Like the IMU pre-integration factor, the residual of the dynamics factor connects consecutive poses and velocities.

Dynamics Model

A simple model of a MAV which considers how the poses evolves according to three forces:

Model translational dynamics using:

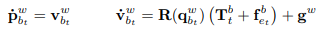
We can estimate the trust vector by calculating the force generated by each motor. This is a function of motor speed and propeller. (Assuming there is a mass normalization not shown in this equation).

Results

Sim (Gazebo)

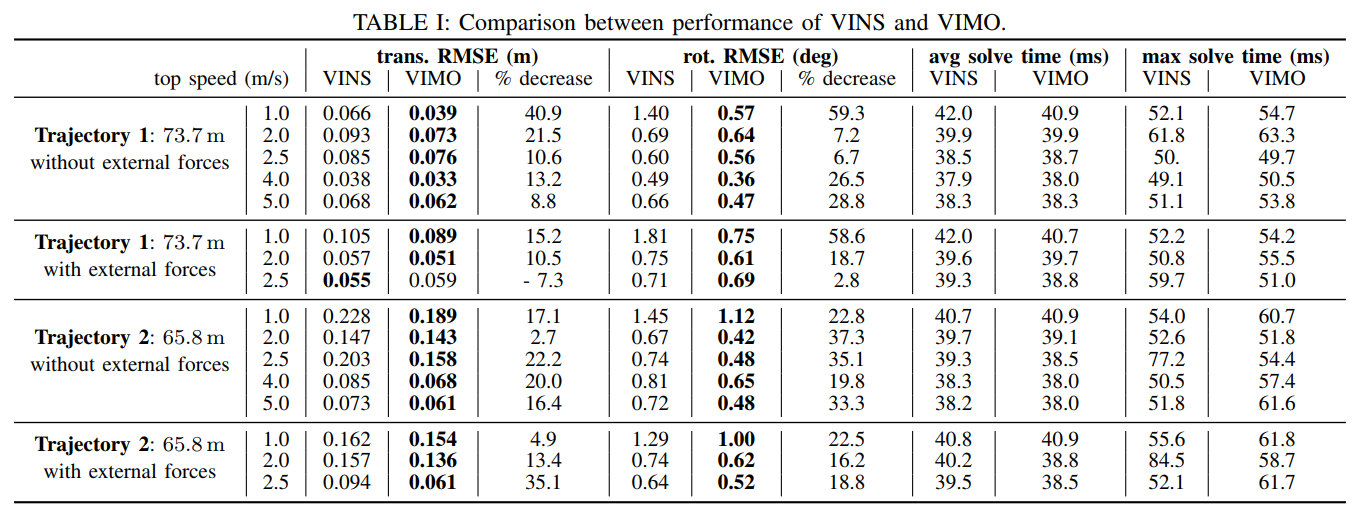
• Accuracy improvement seems to be consistent, but expected in simulated environments

• Force estimation also seems very accurate, but curious about how the varying bias effects the accuracy of force estimation

Blackbird Dataset

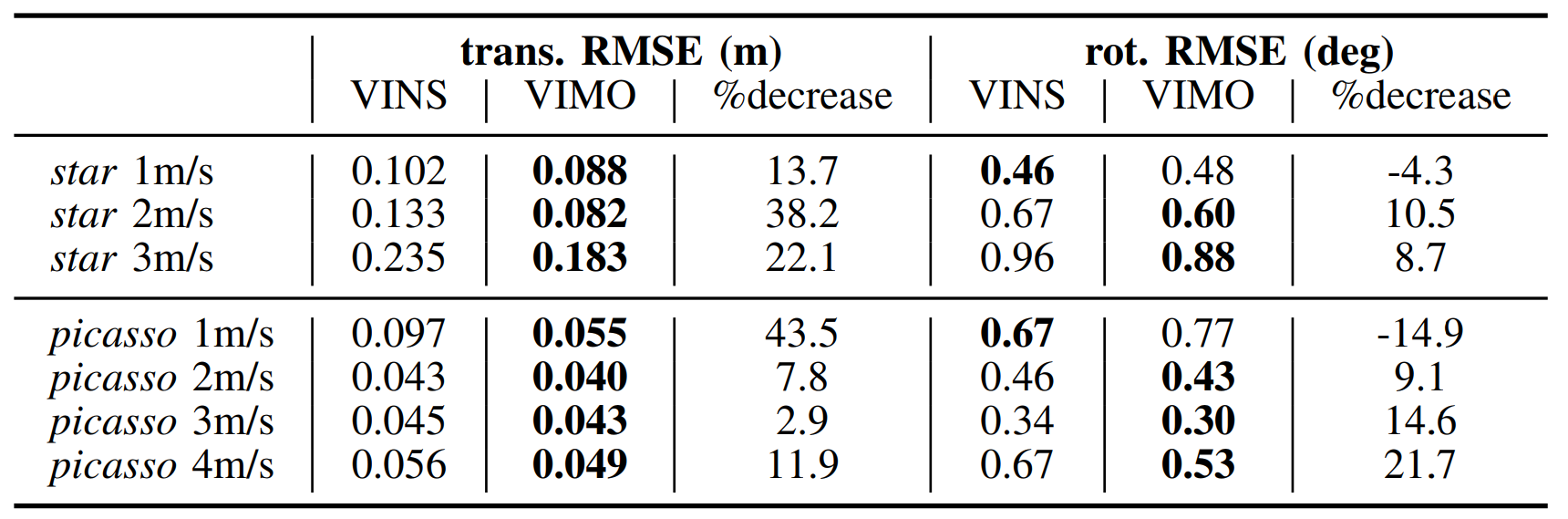
• Blackbird provides rotor speeds and known system dynamics which make it a good candidate for this type of work

Real World

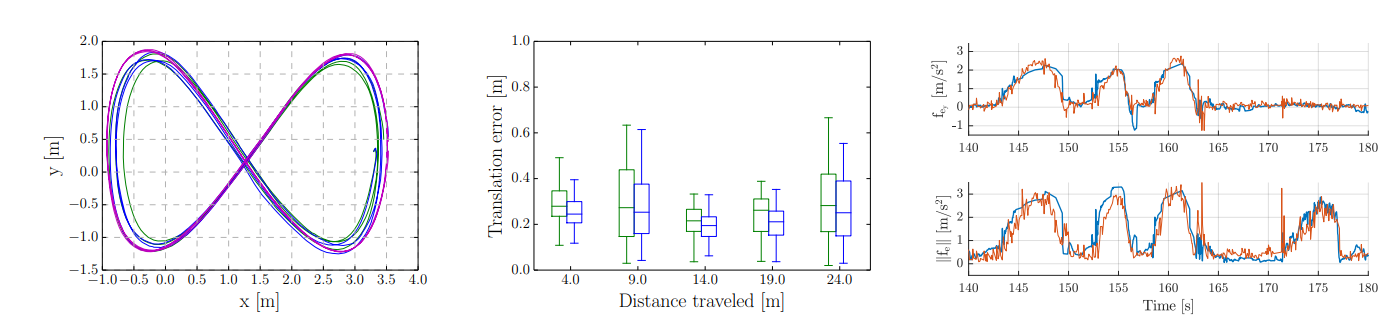
• External force measured using a force measure stick

Thoughts

• Why not model external torques as well?

• There is a strong assumption about the type of external forces that can be observed (zero mean). If there is a constant component to the zero force it is indistinguishable from an IMU accelerometer bias

• In situations where there is a non-zero mean external force, it seems like including dynamics factors would not only result in poor external force estimation but actually degrade the quality of the state estimation
  • This is because the low-frequency components of the external force would be indistinguishable from an IMU bias. This means the bias estimates would be inconsistent.

• In general, how accurate does the dynamics model have to be? Does using an underparameterized or inaccurate model actually hurt state estimation?