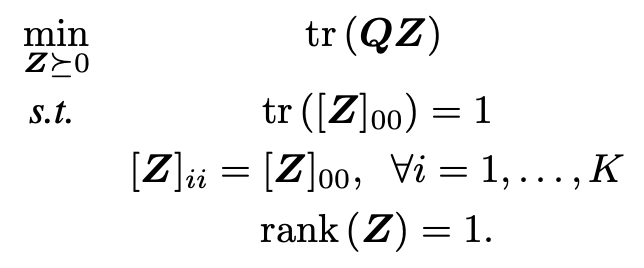TEASER++
Remark
- Registration as a Simultaneous Pose and Correspondence (SPC) problem, in contrast to correspondence-based problems
Quaternion
- Quaternion multiplication can be represented in matrix-vector form, just as cross product
- Quaternion inversion is linear
- Rotating a vector is non-linear
Problem formulation
- Upper bound can be understood as a 3-sigma bound for inlier. No assumption for outliers.
Decoupling
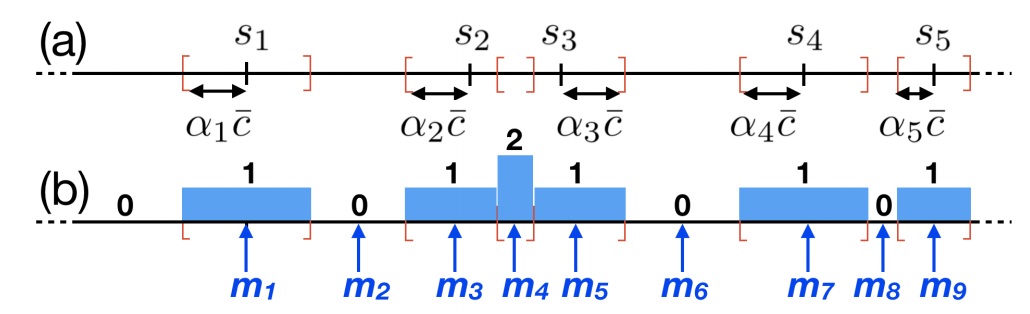
Translation Invariant Measurements (TIMs)
- Insight: relative positions are translation-invariant
- Number of TIMs: N(N-1)/2
- Equivalent with graph representation
- Each vertex is a correspondence
- Each edge is a pair of correspondences

Translation and Rotation Invariant Measurements (TRIMs)
- Insight: norm of relative positions are rotation-invariant
- By dividing ||a_{ij}|| from both sides, we get an expression only depending on s
TEASER
- General comments:
- Input scale is N; all estimations deal with N^2 pairs
- beta is set to 5 cm for TEASER++ in all tests
- Differentiable Hungarian Algorithm
- Heat methods
- Pairwise features? CRF?

- TRIMs for s — TLS estimation
- Algorithm: adpative voting, polynomial time, exact
- s + TIMs for R
- Algorithm: Robust rotation search via tight semidefinite relaxation, polynomial time, exact
is equivalent with
can be rewritten with
with
Now q_k = q for inliers and -q for outliers. It is equivalent to Quadratically-Constrained Quadratic Program:
Q depends on TIMs. Reformat Z with x,
this turns to

3. d + R for t
- Compute t's 3 dimensions independently
Boost performance
- Theorem: Edges corresponding to inlier TIMs form a clique in E0, and there is at least one maximal clique in E0 that contains all the inliers.
- Sparse max-clique can be fast in practice
- An edge (i, j) (and the corresponding TIM) is an inlier if both i and j are correct correspondences
- In practice:
- w max-clique: slow, high performance (90%)
- w/o max-clique: fast, low performance (50%)