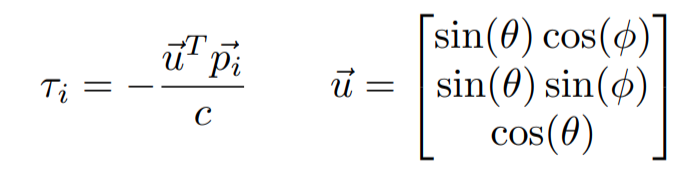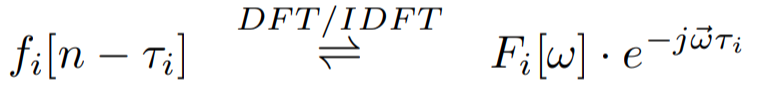Nicholas R. Rypkema, Erin M. Fischell and Henrik Schmidt, MIT, ICRA 2017

Abstract:

• Focused on acoustic localization technique for low cost, small-sized, multi-auv research

• Single, passive acoustic transducer at stationary reference point

• AUV has USBL microphone array using OWTT phased-array beam forming to estimate range and bearing

• Filtering and smoothing is then used to make trajectory estimate consistent

I. Introduction:

• Acc. Localization is essential for path planning & geo-referencing of measurements.

• Underwater environments are challenging due to no GPS, radio, limited bandwidth

• Most AUV's use DVL + periodic GPS to limit error

• These sensors are heavy, large and expensive for small robots, hence focus on low cost MEMS devices such as IMU and compass + acoustics.

• Apart from inertial navigation, 2 techniques
  • Geophysical: Using camera or Sonar systems for SLAM through environmental features (needs clear waters/expensive sensors)
  • Acoustic: Hydrophone and beacon networks. (LBL, SBL, USBL, initial setup cost, usually TWTT, requires hydrophone and transducers on both beacon and receiver)

• Chip-Scale Atomic Clocks, CSAC, allow for OWTT with passive beacons.
  • Eustice et al. Range only OWTT with dead reckoning fusion through MLE
  • Webster et al. Range only OWTT with EKF

• Issue at hand: Singe range only measurement does not give ambiguity free estimate, multiple measurements needed for accuracy.

• OWTT-iUSBL overcomes this issue, inverted means the USBL array is on the AUV rather than fixed beacon.

• Time synchronized clocks between AUV and beacon allow ping times to be known, and recorded acoustic packets are process to find range, azimuth and inclination. If source is fixed, absolute vehicle position can be calculated

II. OWTT IUSBL

A) System Hardware

1. Beacon: Arduino UNO + wave shield connected to GPS unit. GPS Pulse-Per-Second unit triggers playback of 20ms 7-9khz upchirp signal. Played at every GPS second.

2. AUV Reciever: GPS Unit, Data Aq. Module (DAQ), RPi 3, CSAC, the GPS PPS is used to synchronize the CSAC, which makes the DAQ record at 8000 samples/sec. Delay is estimated during calibration by keeping both together initially.

Note: Accurate timing is the most important component for this system. Without it, OWTT passive ranging is not possible. This allows for multiple vehicles to self localize at each time step making it highly scalable. Without a CSAC it is important for both receiver and beacon to communicate and continuously sync times.

B) Matched Filtering

A method for extracting known wavelets from a noisy signal. Cross correlating the template signal with the recorded signal allows to check for actual peak measurement and weed out outliers.

• Recorded wavelets from each of the four hydrophones are used to get a range estimate
  • in essence a convolution between hydrophone i’s received signal $x_i[n]$ and a replica of the up-chirp $h[n]$

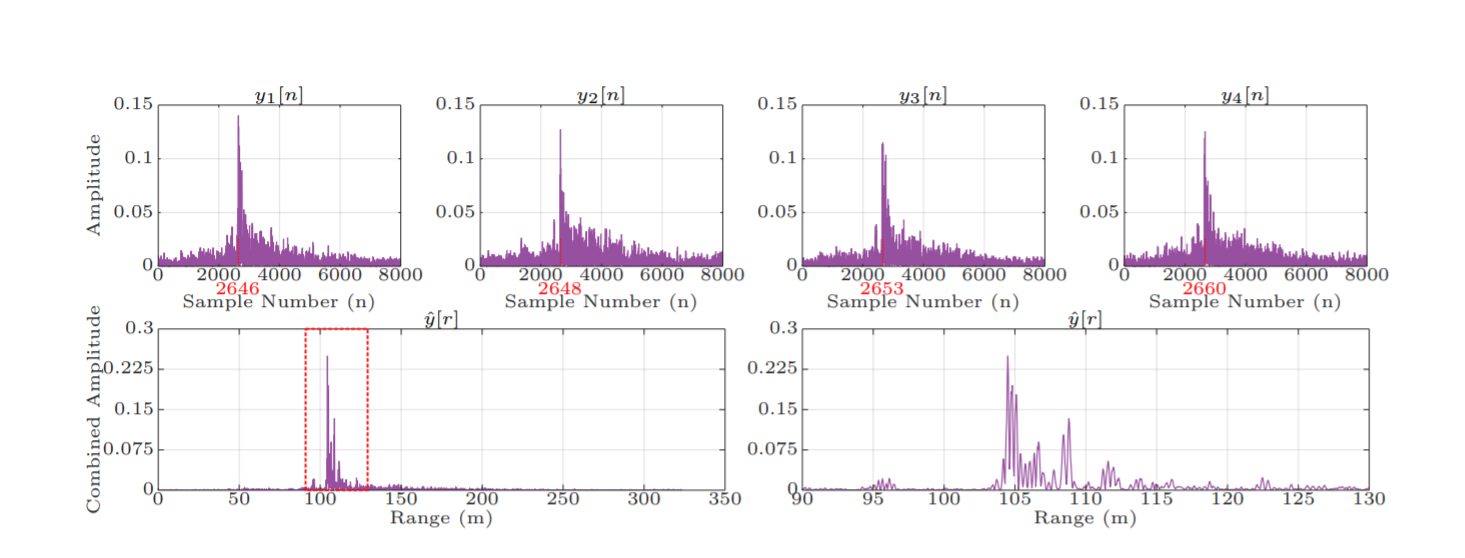
• To account for occlusions which may block some hydrophones from receiving the right signal, a standard deviation of the the arg-max can be used as a validity check

  

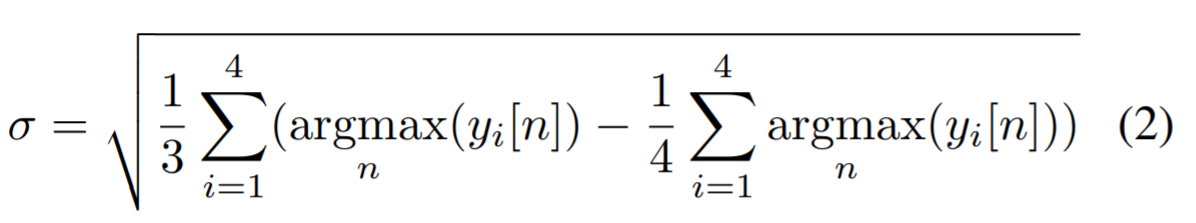
  • If $\sigma < 5$ the measurement is deemed invalid

• Conversion from sample number to range is done by subtracting system delay and scaling ration by velocity of sound over sampling rate:
  • $range (r) = (c/F_s) n = (1480/37500)n$
  • This range estimate is passed to the particle filter.

  C) Phased-Array Beamforming

  • Use raw measurements to build azimuth-inclination (bearing) heatmap by estimating angle of arrival
  • Using array geometry to apply phase shifts or time delays and summing them up.

  (What this means is that given an array of receivers which are arbitrarily arrange in space, there is a plane wave signal onto this alignment from some azimuth and inclination such that a geometric alignment exists that maps these angles to the time at which the signal reaches each receiver).

  • Look angle with max response is likeliest angle of arrival of the incident wave, indicating the 4 signals are in phase and do not cancel each other

  

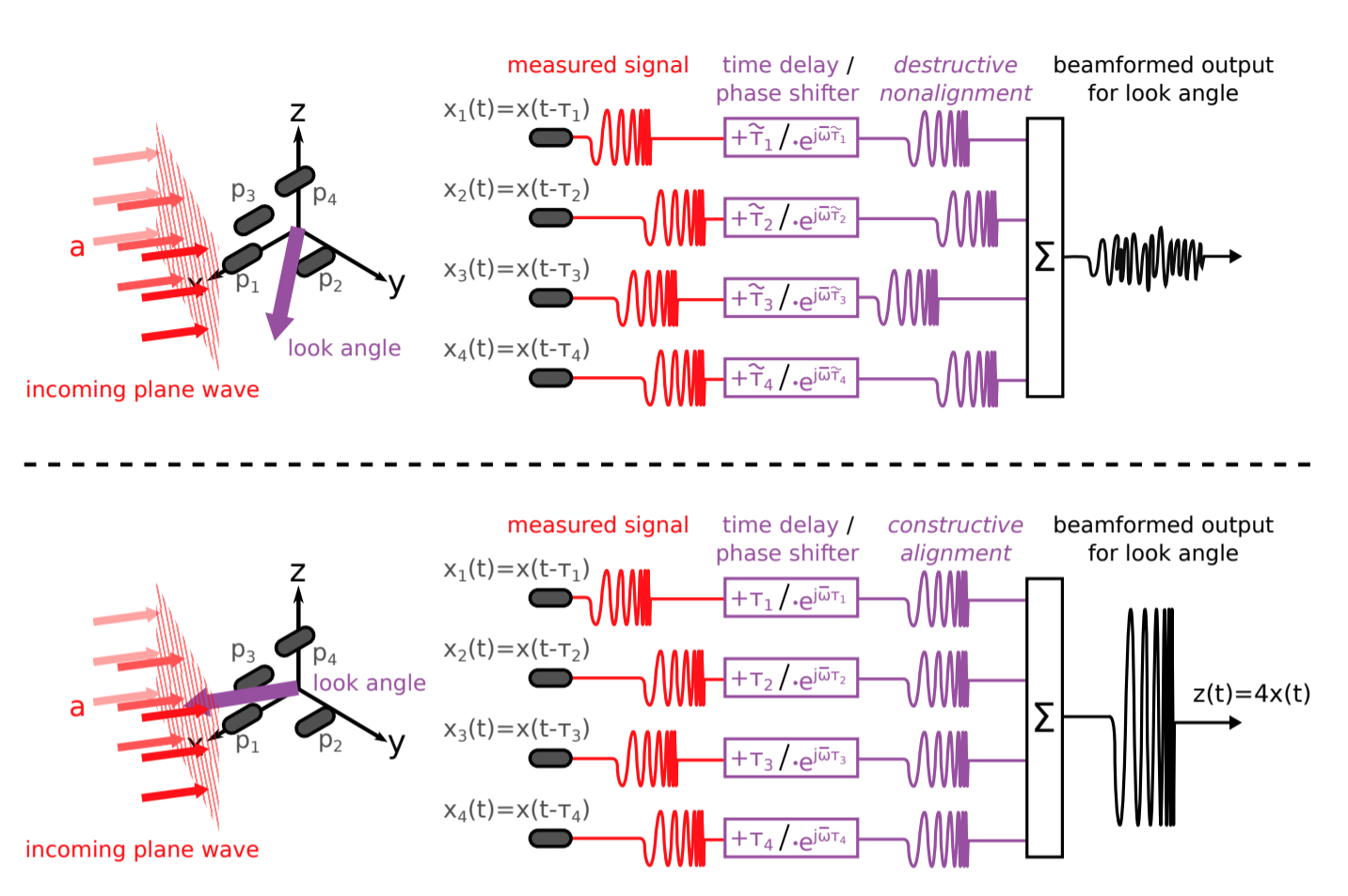
  Top: when the look-angle is not pointing in the opposite direction of the incoming plane wave, nonalignment of the filtered signals result in destructive interference and a low CBF power output.

  Bottom: when the look-angle is pointing exactly in the opposite direction of the incoming plane wave, the filtered signals are aligned, resulting in a scaled reconstruction of the incoming signal and a maximum CBF power output.

  • Time delay, $\tau_i$of a plane is calculated as

  

  $p_i$ is position of hydrophone $i$, $\phi$ and $\theta$ are the look angle azimuth and inclination and c is speed of sound in water. vector $u$ is a unit vector in the opposite direction of propagation.

• The time delay is constant for a look angle and is related to phase shifts in frequency domain as

  

• $f_i$ is the plane wave signal incident on hydrophone $i$ and vector $w$ contains range of frequencies output by n-point Discrete Fourier Transform.

• To reconstruct the plane wave signal while nullifying geometrically induced time delays, they apply opposite phase shifts to the received signals and average over all elements. Matched filtering is again used to ensure accurate signal detection

• The equation below is performing the matched filtering

  

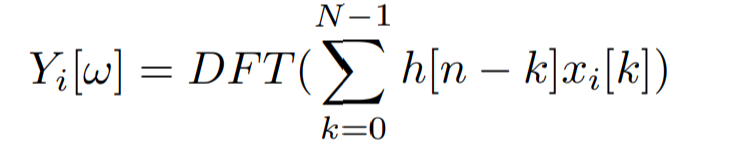
  $x_i[n]$ is the signal received by each hydrophone. The following equation is for the phase shifting and averaging

  

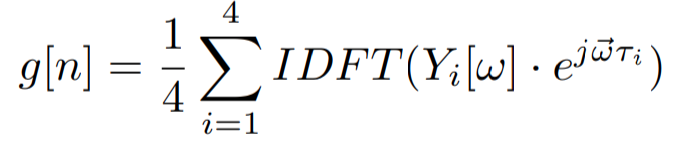
• This produces max response when look angle corresponds to the true angle of arrival. Cycling through all these angles provides an azimuth-inclination heat map. $g[\phi,\theta]$

  

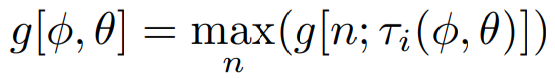
• And the most likely angle of arrival is the maximum of this map.

• Only azimuth angles of 265 - 95 deg and inclination of 45 - 135 deg are considered to account for self occlusion. This is then passed on to the particle filter

• Real time calculations are achieved by using pre-computed phase shift values for each look angle and using Chirp Z transforms instead of a full DFT.

D) Particle Filter Localization

• Matched filtering and beam forming give single estimates for the particular time step, and are noisy due to general resolution and artifacts from reflections. These give non Gaussian outliers

• Particle filters allow for fusion with AUV onboard sensor information and is useful due to non Gaussian nature of noise, hence chosen over EKF

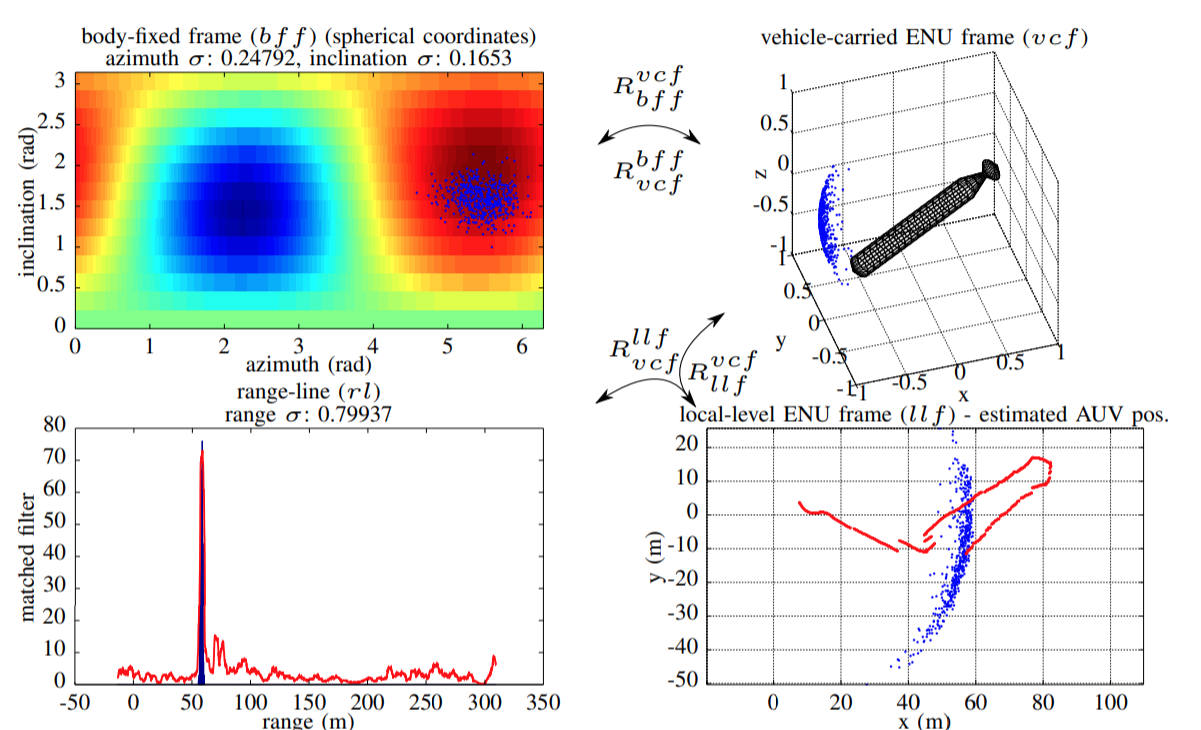
• The filter is over 3 coordinate frames, body fixed(for acoustic), vehicle frame (COG of AUV) and beacon origin.

• Initialization is done during GPS lock in the start. Re-initialization is again performed during new GPS fixes on resurfacing

• Update step: range: Weights multiplied by value of range estimate signal, and resampling and normalization done using systematic resampling.

• Azimuth: Similar, using heat map values but needs coordinate frame transformations

• Estimation step: Weighted means of range and azimuth-elevations in body-fixed frame. Provides an estimate in local level frame relative to beacon.

E) Factor Graph Smoothing

• Particle filter recursively marginalizes out all previous measurements, hence causing discontinuties

• Factor graphs can be used to use all measurements and optimize the trajectory.

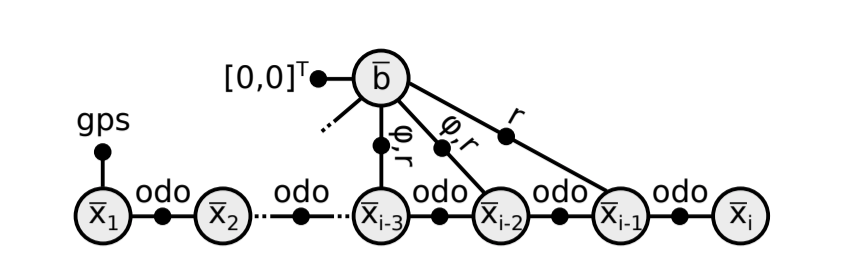
• Estimated pose $vecx_i = [x_i, y_i, \phi_i]^T$ is in local frame.

• GTSAM and iSAM2 are used for MAP inference.

• Motion and measurement noise are assumed to independent and Gaussian, std deviation is estimated from particles in the filter.

III. Experiments and Results

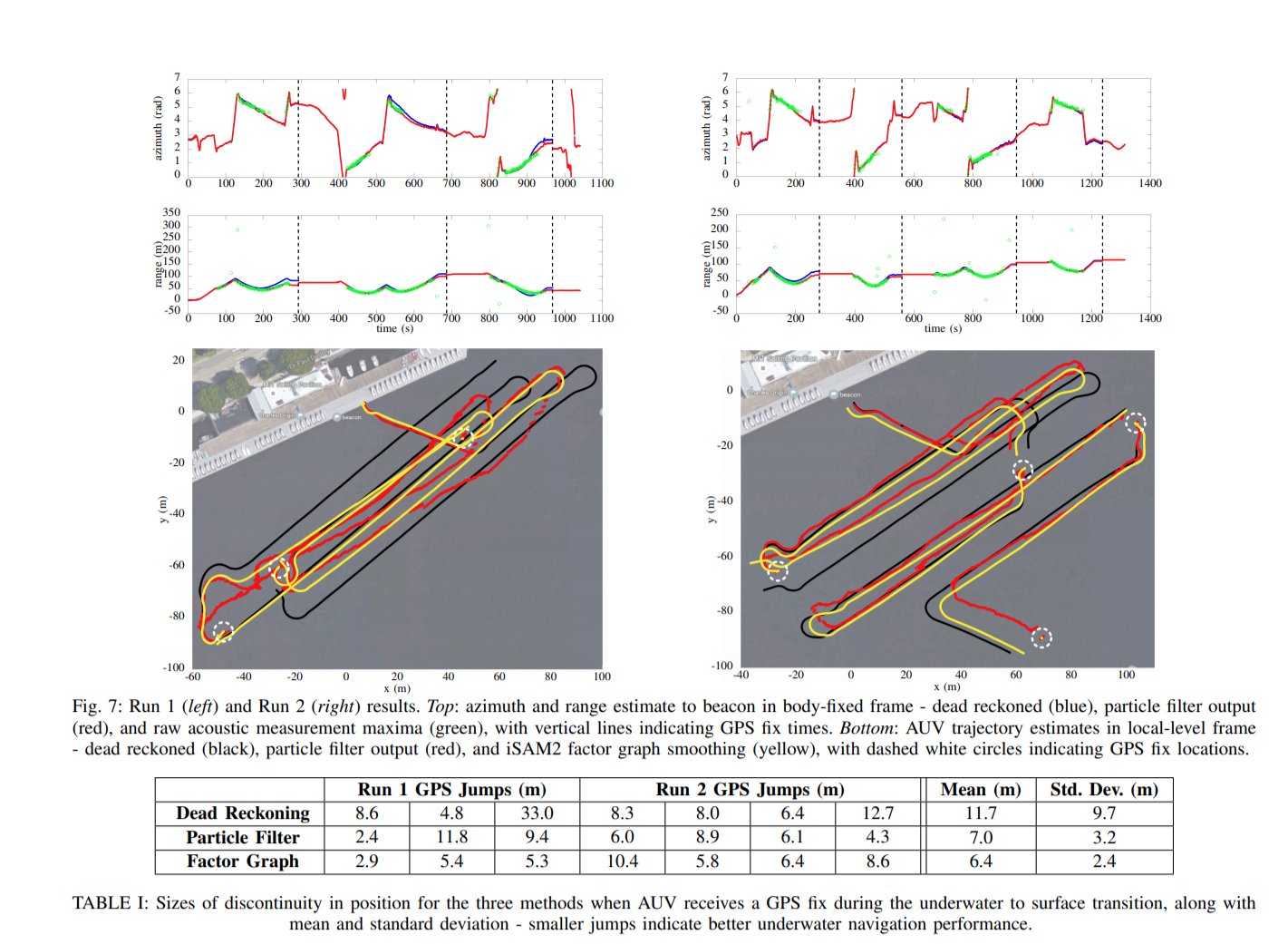
• Conducted at the Charles river, beacon submerged at 0.5m depth

• Preprogrammed mission trajectory at 2m depth with back and forth path of 170m

• GPS fix every 150s and at end of 170m

• RasPi used for matched filtering and phased-array beamforming at 1.25Hz

• Data is recorded, included AUV navigation data which is synced using NTP

• Particle Filtering and factor graph smoothing done offline.

• New graph for each GPS fix, can check difference between estimate and true position at each surfacing

IV. Conclusions

• Single beacon OWTT method shown

• Cheaper than using DVL or INS

• Future work includes using LBL for verification, and online filtering and smoothing